Kinematic Lensing using HI or Optical Linewidths

Kinematic Weak Lensing with Spatially Unresolved Line Widths

Project Status — December 26, 2025

Executive Summary

This project articulates a formalism for kinematic lensing using spatially unresolved line widths (HI 21cm or optical) combined with imaging survey ellipticities, building on Huong et al 2025. The Tully-Fisher relation constrains a disk galaxy's inclination, which determines the magnitude $|\varepsilon_{\rm incl}|$ of its intrinsic ellipticity but not its orientation $\phi_n$. This constrains the gravitational shear $\gamma$ to lie on a ring of radius $R$ in the $(\gamma_1, \gamma_2)$ plane, partially breaking the shape-noise degeneracy.

In particular we incorporate that the information content depends on the ratio $R/\sigma_m$: face-on galaxies ($R \ll \sigma_m$) provide full two-dimensional constraints with no information loss, while only edge-on galaxies suffer the factor-of-4 reduction in power found in variance-based treatments. Since face-on and moderately inclined systems contribute ~95% of the Fisher information, we find gain factors $G \approx 3$ over standard weak lensing for realistic DSA-2000 + Euclid/Roman parameters—corresponding to factor of $\approx 3$ reduction in required sample size for a given shear precision.

Context and Goals

The Shape Noise Problem

Weak gravitational lensing measures the coherent distortion of background galaxy shapes by foreground mass concentrations. The cosmological shear signal is small ($|\gamma| \sim 0.01$–$0.03$), while galaxies have intrinsic ellipticities with dispersion $\sigma_{\rm int} \approx 0.25$–$0.3$ per component. This shape noise is the dominant source of statistical uncertainty in current and future surveys. Precision scales as $\sigma_\gamma \propto \sigma_{\rm int}/\sqrt{N}$, requiring very large samples.

The Kinematic Lensing Idea

If we knew each galaxy's intrinsic ellipticity $\varepsilon_{\rm src}$, we could measure shear directly: $\gamma = \varepsilon_{\rm obs} - \varepsilon_{\rm src}$. For disk galaxies, the intrinsic ellipticity is set by the viewing geometry—specifically the inclination angle $i$. An independent measurement of $i$ (e.g., from the Tully-Fisher relation) partially breaks the shape noise degeneracy.

Two regimes exist:

• Resolved kinematics: Spatially resolved velocity fields (IFU spectroscopy) determine both inclination $i$ and position angle $\phi_n$, fully specifying $\varepsilon_{\rm src}$. Limited to bright, nearby galaxies.
• Unresolved line widths: Integrated HI 21cm profiles constrain $\sin i$ via Tully-Fisher, giving $|\varepsilon_{\rm incl}|$ but not $\phi_n$. Applicable to tens of millions of galaxies with forthcoming radio surveys.

The Opportunity: DSA-2000 + Euclid/Roman

The Deep Synoptic Array (DSA-2000) will detect HI 21cm emission from $>3 \times 10^7$ galaxies over $\sim$30,000 deg², with substantial overlap with Euclid ($\sim$15,000 deg²) and Roman imaging. This creates an unprecedented opportunity:

• Euclid/Roman provide precise shape measurements ($\sigma_m \sim 0.15$–$0.25$) and stellar masses $M_\star$ for Tully-Fisher calibration
• DSA-2000 provides HI line widths (inclination constraints) and precise spectroscopic redshifts
• Combined: Kinematic lensing with $>10^7$ galaxies, independent systematics from radio vs. optical

Goals of This Work

1. Develop the likelihood formalism for shear inference from the ring constraint, going beyond variance-based approximations
2. Quantify the information content as a function of inclination, revealing which galaxies contribute most
3. Calculate realistic gain factors $G$ over standard weak lensing, including finite disk thickness and non-axisymmetry
4. Compare with existing work (Huang et al. 2025) and clarify what is new
5. Provide a foundation for optimal shear estimation pipelines combining radio and optical data

Core Formalism

Ellipticity and Shear

We adopt the standard weak lensing convention for complex ellipticity. For axis ratio $q \leq 1$ and position angle $\phi$:

$$\varepsilon = \varepsilon_1 + i\varepsilon_2 = |\varepsilon| \, e^{2i\phi}, \qquad |\varepsilon| = \frac{1-q}{1+q}$$

In the weak lensing regime, the observed ellipticity relates to source ellipticity and shear by:

$$\varepsilon_{\rm obs} = \gamma + \varepsilon_{\rm src} + \eta$$

where $\eta$ represents measurement noise with variance $\sigma_m^2$.

Inclination from Tully-Fisher

For a thin axisymmetric disk at inclination $i$, the intrinsic ellipticity is:

$$\varepsilon_{\rm src} = \varepsilon_{\rm incl} = |\varepsilon_{\rm incl}| \, e^{2i\phi_n}, \qquad |\varepsilon_{\rm incl}| = \frac{1 - \cos i}{1 + \cos i} \equiv R$$

The Tully-Fisher relation constrains $\sin i$ via the observed HI line width:

$$W_{\rm obs} = W_{\rm TF}(M_\star) \sin i \quad \Rightarrow \quad \sin i = \frac{W_{\rm obs}}{W_{\rm TF}(M_\star)}$$

with intrinsic scatter $\sigma_{\rm TF}$ propagating to fractional uncertainty $\sigma_f$ on $\sin i$.

The Ring Constraint

Combining these relations, the shear is:

$$\gamma = \varepsilon_{\rm obs} - R \, e^{2i\phi_n}$$

Since $\phi_n$ is unknown (uniformly distributed on $[0,\pi)$ for unresolved observations), the shear is constrained to a circle:

$$|\gamma - \varepsilon_{\rm obs}| = R$$

with center at $\varepsilon_{\rm obs}$ and radius $R = |\varepsilon_{\rm incl}|$ determined from the line width.

The Ring Likelihood

Single Galaxy

The likelihood for shear $\gamma$ given observed ellipticity and ring radius is obtained by marginalizing over $\phi_n$:

$$\mathcal{L}(\gamma \,|\, \varepsilon_{\rm obs}, R) = \int_0^\pi \frac{d\phi_n}{\pi} \, \frac{1}{2\pi\sigma_m^2} \exp\left[-\frac{|\varepsilon_{\rm obs} - \gamma - R e^{2i\phi_n}|^2}{2\sigma_m^2}\right]$$

Defining $d \equiv |\varepsilon_{\rm obs} - \gamma|$ and evaluating the integral yields the Bessel likelihood:

$$\mathcal{L}(\gamma) \propto \exp\left[-\frac{d^2 + R^2}{2\sigma_m^2}\right] \, I_0\left(\frac{dR}{\sigma_m^2}\right)$$

where $I_0$ is the modified Bessel function of the first kind. This likelihood is not Gaussian—it is ring-shaped, peaked at $d = R$.

Limiting Regimes

Face-on limit ($R \ll \sigma_m$): Using $I_0(x) \approx 1$ for small $x$:

$$\mathcal{L}(\gamma) \propto \exp\left[-\frac{d^2}{2\sigma_m^2}\right]$$

This is a standard 2D Gaussian—the ring degenerates to a point.

Edge-on limit ($R \gg \sigma_m$): Using $I_0(x) \approx e^x/\sqrt{2\pi x}$ for large $x$:

$$\log \mathcal{L}(\gamma) \approx -\frac{(d - R)^2}{2\sigma_m^2} + \text{const}$$

The likelihood is sharply peaked on the ring $d = R$, constraining only the radial direction.

Including Tully-Fisher Uncertainty

The TF scatter $\sigma_f$ propagates to uncertainty on $R$:

$$\sigma_{\sin i} = \sin i \cdot \sigma_f, \qquad \sigma_{\cos i} = \frac{\sin^2 i}{\cos i} \sigma_f$$

Through the chain $\sin i \to \cos i \to R$:

$$\sigma_R = \frac{2R(1+R)}{1-R} \cdot \sigma_f \cdot \frac{\sin i}{\cos i}$$

This diverges for edge-on galaxies ($\cos i \to 0$), explaining their negligible information contribution.

The total radial uncertainty combines measurement noise and TF scatter:

$$\sigma_{\rm rad}^2 = \sigma_m^2 + \sigma_R^2$$

Combined Likelihood for Multiple Galaxies

For $N$ galaxies in a local region probing a common shear $\gamma$:

$$\log \mathcal{L}(\gamma) = \sum_{i=1}^N \left[ -\frac{d_i^2 + R_i^2}{2\sigma_m^2} + \log I_0\left(\frac{d_i R_i}{\sigma_m^2}\right) \right]$$

This is a sum of "ring potentials"—the maximum likelihood $\hat{\gamma}$ occurs where the rings best intersect.

Fisher Information

The Rank-1 Structure

In the sharp-ring limit, the Fisher matrix for a single galaxy is rank-1:

$$\mathbf{F} = \frac{1}{\sigma_{\rm rad}^2} \, \hat{n} \otimes \hat{n}, \qquad \hat{n} = (\cos 2\phi_n, \sin 2\phi_n)$$

This constrains only the radial direction; the tangential direction (along the ring) is unconstrained.

The $n_{\rm eff}$ Formula

The Fisher information per galaxy depends on $R/\sigma_m$, interpolating between face-on and edge-on limits:

$$F = \frac{n_{\rm eff}}{2(\sigma_m^2 + \sigma_R^2)}, \qquad n_{\rm eff} = 1 + \frac{1}{1 + R^2/\sigma_m^2}$$

Face-on ($R \to 0$):
$n_{\rm eff} = 2$
$F = 1/(\sigma_m^2 + \sigma_R^2)$
Full 2D information

Edge-on ($R \gg \sigma_m$):
$n_{\rm eff} \to 1$
$F = 1/[2(\sigma_m^2 + \sigma_R^2)]$
Rank-1 (factor of 2 in Fisher)

Combining $N$ Galaxies

For random orientations $\{\phi_{n,i}\}$, the averaged Fisher matrix becomes diagonal:

$$\langle \mathbf{F}_{\rm tot} \rangle = \sum_{i=1}^N \frac{n_{{\rm eff},i}}{2(\sigma_m^2 + \sigma_{R,i}^2)} \, \mathbf{I}$$

Individual rank-1 constraints sum to full-rank when galaxies have diverse $\phi_n$.

Standard Weak Lensing Comparison

Without kinematic information, the intrinsic ellipticity is unknown with population variance $\sigma_{\rm int}^2$:

$$F_{\rm std} = \frac{N}{\sigma_m^2 + \sigma_{\rm int}^2}, \qquad \sigma_{\rm int}^2 = \langle R^2 \rangle = 3 - 4\ln 2 \approx 0.227$$

The Gain Factor

$$G \equiv \frac{F_{\rm kin}}{F_{\rm std}} = (\sigma_m^2 + \sigma_{\rm int}^2) \left\langle \frac{n_{\rm eff}}{2(\sigma_m^2 + \sigma_R^2)} \right\rangle$$

For an isotropic inclination distribution ($\cos i$ uniform on $[0,1]$), the population average becomes:

$$G = (\sigma_m^2 + \sigma_{\rm int}^2) \int_0^1 \frac{n_{\rm eff}(x)}{2[\sigma_m^2 + \sigma_R^2(x)]} \, dx$$

where $x = \cos i$, $R(x) = (1-x)/(1+x)$, and $\sigma_R(x) = 2R(1+R)/(1-R) \cdot \sigma_f \sqrt{1-x^2}/x$.

Realistic Disk Properties

Finite Thickness

Real disks have intrinsic thickness $q_0 \sim 0.2$. The observed axis ratio becomes:

$$q^2 = q_0^2 + (1 - q_0^2) \cos^2 i$$

modifying the ellipticity–inclination relation:

$$R(i; q_0) = \frac{1 - q(i; q_0)}{1 + q(i; q_0)}$$

Key effects: $R_{\rm max} \approx 0.67$ for $q_0 = 0.2$ (not 1.0); face-on disks have $R_{\rm min} \approx 0.09$ (not 0).

Non-Axisymmetry

Bars, spirals, and warps add ellipticity not captured by the inclination model:

$$\sigma_{\rm rad}^2 \to \sigma_m^2 + \sigma_R^2 + \sigma_{\rm disk}^2$$

with $\sigma_{\rm disk} \sim 0.05$ from empirical constraints.

Numerical Results

Gain Factors — Idealized Thin Disks

$\sigma_f$	$\sigma_m = 0.10$	$\sigma_m = 0.15$	$\sigma_m = 0.20$	$\sigma_m = 0.25$
0.00	14.6	7.3	4.6	3.4
0.05	8.5	4.8	3.3	2.6
0.10	7.4	4.3	3.0	2.4
0.15	6.7	4.0	2.8	2.3
0.20	6.2	3.7	2.7	2.2

Highlighted: DSA-2000 realistic range ($\sigma_f \approx 0.10$–$0.15$)

Gain Factors — Realistic Disks ($q_0=0.2$, $\sigma_{\rm disk}=0.05$)

$\sigma_f$	$\sigma_m = 0.10$	$\sigma_m = 0.15$	$\sigma_m = 0.20$	$\sigma_m = 0.25$
0.00	8.0	4.6	3.2	2.4
0.05	5.7	3.7	2.7	2.1
0.10	4.8	3.2	2.4	2.0
0.15	4.2	2.9	2.2	1.9
0.20	3.9	2.7	2.1	1.8

Information Budget by Inclination

For $\sigma_m = 0.2$, $\sigma_f = 0.1$ (thin disk):

Inclination Range	Fraction of Total Information
Face-on ($i < 26°$)	25%
Low inclination ($26° < i < 46°$)	44%
Moderate ($46° < i < 60°$)	26%
High inclination ($60° < i < 73°$)	5%
Edge-on ($i > 73°$)	<1%

Key result: Face-on and moderate-inclination galaxies ($i < 60°$) provide ~95% of the total information, despite edge-on systems comprising 30% of the sample by solid angle. This is because $\sigma_R \to \infty$ as $\cos i \to 0$.

Comparison with Huang, Krause et al. (2025)

Reference: arXiv:2510.18011

Aspect	Huang et al.	This Work
Basic constraint	$\gamma = \varepsilon_{\rm obs} - |\varepsilon_{\rm incl}|e^{2i\phi}$ Same	Identical equation
Methodology	Correlation functions $\xi_\pm$	Per-galaxy Bessel likelihood New
Information loss	Uniform factor-of-4 in $C_\ell$	$R$-dependent $n_{\rm eff}$ New
Face-on galaxies	Same penalty as edge-on	Full 2D, no penalty New
Galaxy weighting	Uniform	Optimal: $\propto n_{\rm eff}/\sigma_{\rm rad}^2$ New

Both approaches recover consistent results when properly compared. The likelihood formalism reveals that the factor-of-4 applies only to edge-on systems; face-on galaxies escape this penalty entirely. Since they dominate the information budget, the population-averaged gain exceeds naive factor-of-4 estimates.

File Inventory

LaTeX Paper

• kinematic_lensing_paper_v2.tex — Main paper (13 pages)
• kinematic_lensing_paper_v2.pdf — Compiled PDF

Figures

• figure1_ring_constraint.png/pdf — Ring geometry schematic
• figure2_gain_factor_v2.png/pdf — $G$ vs $\sigma_f$

Code & Documentation

• kinematic_lensing_figures_v2.ipynb — Figure generation notebook
• CLAUDE.md — Context file for Claude Code

Fiducial Parameters

Parameter	Symbol	Value	Source
Shape measurement noise	$\sigma_m$	0.15–0.25	Euclid/Roman
TF fractional scatter	$\sigma_f$	0.10–0.15	HI surveys
Disk thickness	$q_0$	0.15–0.25	Observations
Non-axisymmetry	$\sigma_{\rm disk}$	0.03–0.07	Bars/spirals
Galaxy count	$N$	$>10^7$	DSA-2000
Sky overlap	—	~15,000 deg²	Euclid $\cap$ DSA

Fiducial result: $\sigma_m = 0.20$, $\sigma_f = 0.12$, $q_0 = 0.2$, $\sigma_{\rm disk} = 0.05$ $\;\Rightarrow\;$ $G \approx 2.3$

Future Directions

Theory

• Full likelihood MCMC shear inference
• Modified $\xi_\pm$ with $n_{\rm eff}$ weighting
• Intrinsic alignment mitigation
• TF evolution $\sigma_f(z)$

Applications

• DSA-2000 detailed forecasts
• SKA comparison
• Optical emission lines (H$\alpha$, [OII])
• Cosmological parameter forecasts

Key References

• Huang et al. (2025), arXiv:2510.18011 — One-component KL, SKA2 forecasts
• Huff et al. (2013), MNRAS 431, 1629 — "Kinematic lensing" terminology
• Blain (2002), ApJ 570, L51 — First KL proposal
• Gurri et al. (2020), MNRAS 499, 4591 — First KL measurement
• Hallinan et al. (2019), BAAS 51, 255 — DSA-2000

---

Developed in conversation between H.-W. Rix and Claude (Anthropic), December 2025.

RR Lyrae in the inner Galaxy

At the last group meeting we discussed several issues revolving around RRL in the galaxy. a) Maddie Lucey's paper: she did the selection function using the Rybizki and Drimmel trick. Do we have to do it a la Cantat-Gauding, with the VIVACE and DES as the 'ground-truth' sample b) the poor old heart and RRL. The Vivace sample shows a tight know of RRL at the very center. The distance modulus spread (after extinction correction) is only sigma = 0.25mag. Or 12% of 1.0 kpc at 8.1 kpc. Plan: do light-curved based metallicities and get the spatial structure...

Constraining chemical yield delay-time distributions with abundance-age data

Constraining Delay Time Distributions from Observed Age-Abundance Relations: A Single-Zone Chemical Evolution Approach

Abstract

We present a method for constraining the delay time distribution (DTD) of element X from observed stellar abundance patterns. Using the single-zone chemical evolution framework of Weinberg et al. (2017), we derive the DTD that produces a linear increase in \([\text{X/Mg}]\) with stellar age for stars at solar magnesium abundance (\([\text{Mg/H}] = 0\)). We find that achieving such a linear trend requires a DTD that increases with delay time, compensating for the declining star formation history. This mathematical framework provides a direct link between observable age-abundance relations and the underlying nucleosynthetic delay times.

1. Introduction

The chemical abundances of stars encode the enrichment history of their birth environments. For elements produced on different timescales, abundance ratios can serve as "chemical clocks" that trace the temporal evolution of galaxies. A particularly powerful diagnostic is the ratio \([\text{X/Mg}]\), where Mg is produced essentially instantaneously by core-collapse supernovae (CCSNe), while element X may have both instantaneous and delayed production channels.

The key question we address is: Can chemical evolution models constrain the delay time distribution (DTD) of element X from observed age-abundance relations? Specifically, we consider stars with solar magnesium abundance (\([\text{Mg/H}] = 0\)) and examine how their \([\text{X/Mg}]\) ratios vary with stellar age. This approach builds on the single-zone chemical evolution framework developed by Weinberg et al. (2017), which provides analytic solutions for abundance evolution with realistic delay time distributions.

In this work, we:

1. Adapt the Weinberg et al. (2017) framework to the specific case of \([\text{X/Mg}]\) evolution
2. Derive the mathematical relationship between observed age-\([\text{X/Mg}]\) trends and the underlying DTD
3. Solve for the DTD that produces a linear increase in \([\text{X/Mg}]\) with stellar age

2. Single-Zone Chemical Evolution Framework

2.1 Basic Equations

Following Weinberg et al. (2017), we consider a one-zone model where metals are instantaneously mixed throughout the star-forming gas. The evolution of element masses is governed by:

\[\dot{M}_{\text{Mg}} = m^{\text{cc}}_{\text{Mg}} \dot{M}_* - (1 + \eta - r) \dot{M}_* Z_{\text{Mg}}\]

\[\dot{M}_{\text{X}} = m^{\text{cc}}_{\text{X}} \dot{M}_* + m^{\text{delayed}}_{\text{X}} \langle\dot{M}_*\rangle_f - (1 + \eta - r) \dot{M}_* Z_{\text{X}}\]

where:

• \(\dot{M}_*\) is the star formation rate
• \(m^{\text{cc}}_{\text{Mg}}\) and \(m^{\text{cc}}_{\text{X}}\) are the instantaneous yields from CCSNe
• \(m^{\text{delayed}}_{\text{X}}\) is the delayed yield of element X
• \(\eta\) is the outflow mass loading factor
• \(r\) is the recycling fraction
• \(Z_i = M_i/M_g\) is the mass fraction of element \(i\)

The delayed production term involves the time-averaged star formation rate:

\[\langle\dot{M}_*(t)\rangle_f = \frac{\int_0^t \dot{M}_*(t') f(t-t') dt'}{\int_0^{\infty} f(\tau) d\tau}\]

where \(f(\tau)\) is the delay time distribution we seek to constrain.

2.2 Solutions for Exponential Star Formation History

For an exponentially declining star formation history, \(\dot{M}_*(t) = \dot{M}_{*,0} e^{-t/\tau_{\text{sfh}}}\), Weinberg et al. (2017) show that the equilibrium abundances are:

\[Z_{\text{Mg,eq}} = \frac{m^{\text{cc}}_{\text{Mg}}}{1 + \eta - r - \tau_*/\tau_{\text{sfh}}}\]

\[Z_{\text{X,eq}} = \frac{m^{\text{cc}}_{\text{X}} + m^{\text{delayed}}_{\text{X}} \cdot \text{DF}_{\infty}}{1 + \eta - r - \tau_*/\tau_{\text{sfh}}}\]

where \(\tau_* = M_g/\dot{M}_*\) is the star formation efficiency timescale and \(\text{DF}_{\infty}\) is the asymptotic value of the delayed factor.

2.3 The Delayed Factor

The delayed factor, which encodes the contribution from delayed production, is:

\[\text{DF}(t) = \frac{\langle\dot{M}_*(t)\rangle_f}{\dot{M}_*(t)} = e^{t/\tau_{\text{sfh}}} \int_0^t f(\tau) e^{-\tau/\tau_{\text{sfh}}} d\tau\]

This factor evolves from 0 at \(t=0\) (no delayed contribution) to some asymptotic value as \(t \to \infty\).

3. Connecting Observables to Theory

3.1 The Age-Metallicity Relation

Stars inherit the gas-phase abundances at their formation time. Therefore:

• Old stars (large age \(\tau_{\text{age}}\)) formed at small \(t\) when \([\text{X/Mg}]\) was low
• Young stars (small \(\tau_{\text{age}}\)) formed at large \(t\) when \([\text{X/Mg}]\) was high

The relationship between stellar age and formation time is:

\[t_{\text{form}} = t_{\text{now}} - \tau_{\text{age}}\]

3.2 The [X/Mg] Ratio

The abundance ratio at any time is:

\[\text{[X/Mg]}(t) = \log_{10}\left(\frac{Z_{\text{X}}(t)}{Z_{\text{Mg}}(t)}\right) = \log_{10}\left(\frac{m^{\text{cc}}_{\text{X}} + m^{\text{delayed}}_{\text{X}} \cdot \text{DF}(t)}{m^{\text{cc}}_{\text{Mg}}}\right)\]

This can be rewritten as:

\[\text{[X/Mg]}(t) = \text{[X/Mg]}_{\text{initial}} + \log_{10}\left(1 + \frac{m^{\text{delayed}}_{\text{X}}}{m^{\text{cc}}_{\text{X}}} \cdot \text{DF}(t)\right)\]

4. Constraining the DTD from Observations

4.1 The Inverse Problem

Given an observed relation \([\text{X/Mg}] = F(\tau_{\text{age}})\) for stars with \([\text{Mg/H}] = 0\), we want to find the DTD \(f(\tau)\) that reproduces this relation.

For stars with \([\text{Mg/H}] = 0\), we know that:

\[Z_{\text{Mg}}(t_{\text{form}}) = Z_{\text{Mg},\odot}\]

This constraint determines when each star formed, allowing us to convert the age-abundance relation into a time-abundance relation.

4.2 Linear Age-[X/Mg] Relation

Consider the specific case where \([\text{X/Mg}]\) increases linearly with age:

\[\text{[X/Mg]}(\tau_{\text{age}}) = A + B \cdot \tau_{\text{age}}\]

where \(A\) and \(B\) are constants determined by observations. Converting to formation time:

\[\text{[X/Mg]}(t_{\text{form}}) = A + B \cdot (t_{\text{now}} - t_{\text{form}}) = (A + B \cdot t_{\text{now}}) - B \cdot t_{\text{form}}\]

This requires \([\text{X/Mg}]\) to decrease linearly with formation time.

4.3 Required Delayed Factor Evolution

From the expression for \([\text{X/Mg}]\), we need:

\[\log_{10}\left(1 + \frac{m^{\text{delayed}}_{\text{X}}}{m^{\text{cc}}_{\text{X}}} \cdot \text{DF}(t)\right) = C - B \cdot t\]

where \(C\) is a constant. Taking the antilog:

\[1 + \frac{m^{\text{delayed}}_{\text{X}}}{m^{\text{cc}}_{\text{X}}} \cdot \text{DF}(t) = 10^{C - B \cdot t}\]

Solving for the delayed factor:

\[\text{DF}(t) = \frac{m^{\text{cc}}_{\text{X}}}{m^{\text{delayed}}_{\text{X}}} \left(10^{C - B \cdot t} - 1\right)\]

5. Deriving the Delay Time Distribution

5.1 The Integral Equation

From the definition of the delayed factor:

\[\text{DF}(t) = e^{t/\tau_{\text{sfh}}} \int_0^t f(\tau) e^{-\tau/\tau_{\text{sfh}}} d\tau\]

Taking the derivative:

\[\frac{d\text{DF}}{dt} = \frac{1}{\tau_{\text{sfh}}} \text{DF}(t) + f(t)\]

Solving for \(f(t)\):

\[f(t) = \frac{d\text{DF}}{dt} - \frac{1}{\tau_{\text{sfh}}} \text{DF}(t)\]

5.2 Solution for Linear [X/Mg] Growth

For the delayed factor derived above:

\[\frac{d\text{DF}}{dt} = -B \ln(10) \cdot \frac{m^{\text{cc}}_{\text{X}}}{m^{\text{delayed}}_{\text{X}}} \cdot 10^{C - B \cdot t}\]

Substituting into the expression for \(f(t)\):

\[f(t) = \frac{m^{\text{cc}}_{\text{X}}}{m^{\text{delayed}}_{\text{X}}} \left[-B \ln(10) \cdot 10^{C - B \cdot t} - \frac{1}{\tau_{\text{sfh}}} \left(10^{C - B \cdot t} - 1\right)\right]\]

5.3 Key Mathematical Insight

For typical parameter values where \(B > 0\) (older stars have lower \([\text{X/Mg}]\)):

• The first term dominates and is negative
• This implies \(f(t) < 0\) for some range of \(t\)
• A negative DTD is unphysical!

This paradox arises because we're trying to achieve a decreasing \([\text{X/Mg}]\) with formation time despite an exponentially declining SFH. The resolution requires a modified approach.

6. Physical DTD Solutions

6.1 Compensating for Declining SFH

To achieve increasing \([\text{X/Mg}]\) with decreasing age (decreasing with formation time), the DTD must compensate for the exponentially declining star formation. The required form is:

\[f(\tau) = g(\tau) \cdot \frac{e^{\tau/\tau_{\text{sfh}}}}{\tau_{\text{sfh}}}\]

where \(g(\tau)\) is a normalized distribution. The exponential factor exactly cancels the weighting from the declining SFH, giving:

\[\text{DF}(t) = \int_0^t g(\tau) d\tau = G(t)\]

where \(G(t)\) is the cumulative distribution function of \(g(\tau)\).

6.2 Power-Law Family of Solutions

For a smooth transition from \(\text{DF}(0) = 0\) to \(\text{DF}(t_{\text{max}}) = 1\), consider:

\[g(\tau) = \frac{(n+1)\tau^n}{t_{\text{max}}^{n+1}} \quad \text{for } 0 < \tau < t_{\text{max}}\]

This gives:

\[G(t) = \left(\frac{t}{t_{\text{max}}}\right)^{n+1}\]

The complete DTD is:

\[\boxed{f(\tau) = \frac{(n+1)\tau^n}{t_{\text{max}}^{n+1}} \cdot \frac{e^{\tau/\tau_{\text{sfh}}}}{\tau_{\text{sfh}}}}\]

6.3 Linear [X/Mg] Growth

For exactly linear growth in \([\text{X/Mg}]\) with age, we need \(\text{DF}(t) \propto t\), which requires \(n = 0\):

\[f(\tau) = \frac{1}{t_{\text{max}}} \cdot \frac{e^{\tau/\tau_{\text{sfh}}}}{\tau_{\text{sfh}}}\]

This DTD:

• Increases exponentially with delay time
• Peaks at late times
• Provides uniform enrichment rate despite declining SFH

7. Discussion

7.1 Physical Interpretation

The derived DTD that increases with delay time is unusual compared to typical astrophysical delay distributions (e.g., Type Ia SNe, which decline as \(t^{-1.1}\)). Possible physical scenarios include:

1. Metallicity-dependent yields: If element X production efficiency increases with metallicity, later generations contribute more
2. Multiple sources: A combination of sources with different characteristic timescales
3. Mass-dependent delays: If lower-mass stars (with longer lifetimes) are more efficient X producers

7.2 Observational Tests

To apply this framework:

1. Measure \([\text{X/Mg}]\) vs age for a sample of stars with \([\text{Mg/H}] \approx 0\)
2. Fit the functional form of the age-abundance relation
3. Use the derived expressions to constrain the DTD
4. Compare with theoretical predictions for various nucleosynthetic sources

7.3 Limitations

This analysis assumes:

• Perfect mixing (one-zone approximation)
• Constant star formation efficiency
• No radial flows or stellar migration
• Metallicity-independent yields

Relaxing these assumptions would require more complex models but could provide additional constraints on the DTD.

8. Conclusions

We have developed a mathematical framework for constraining delay time distributions from observed age-abundance relations in stellar populations. The key findings are:

1. Observable \([\text{X/Mg}]\) trends with stellar age directly encode information about the DTD of element X
2. For stars at fixed \([\text{Mg/H}]\), the age-abundance relation can be inverted to derive the required DTD
3. Achieving a linear increase in \([\text{X/Mg}]\) with age requires a DTD that increases exponentially with delay time
4. This unusual form compensates for the declining star formation history to maintain steady enrichment

This framework provides a direct link between observable stellar abundances and the underlying physics of nucleosynthesis, offering a new tool for understanding the origin of elements.

Acknowledgments

We thank...

References

Weinberg, D. H., Andrews, B. H., & Freudenburg, J. 2017, ApJ, 837, 183

Binary Stars and Gravitational Waves

Gravitational waves (GWs) offer a unique probe into compact binary systems. Non-merging white dwarf (WD) binaries—systems that emit continuous, nearly monochromatic GWs without merging within a Hubble time—are significant sources in the milli-Hertz frequency range, observable by LISA. Here we summarize results for GW strain amplitude from such binaries and details how LISA determines their distance and sky position, with exhaustive derivations and examples.

1. Derivation of the GW Signal

Consider two white dwarfs with masses \( M_1 \) and \( M_2 \), orbiting circularly with period \( P \), at a luminosity distance \( D \) from Earth. We use the quadrupole approximation in the non-relativistic limit to compute the GW strain.

Step 1: Define Orbital Parameters

The orbital dynamics are foundational to the GW signal. Define the following:

• Orbital Angular Frequency (\( \omega \)):
  \[ \omega = \frac{2\pi}{P}, \]
  where \( P \) is the orbital period in seconds, and \( \omega \) is in radians per second. This relates the frequency of rotation to the time for one complete orbit.
• Total Mass (\( M \)):
  \[ M = M_1 + M_2, \]
  the sum of the individual masses in kilograms, governing the system's gravitational interaction.
• Reduced Mass (\( \mu \)):
  \[ \mu = \frac{M_1 M_2}{M_1 + M_2}, \]
  a measure of the effective mass for the two-body problem, also in kilograms, which influences the GW amplitude.
• Orbital Separation (\( a \)): Apply Kepler's third law for a circular orbit:
  \[ P = 2\pi \sqrt{\frac{a^3}{G M}}, \]
  where \( G \) is the gravitational constant (\( 6.67430 \times 10^{-11} \, \text{m}^3 \text{kg}^{-1} \text{s}^{-2} \)). Square both sides:
  \[ P^2 = \frac{4\pi^2 a^3}{G M}. \]
  Rearrange for \( a^3 \) and take the cube root:
  \[ a = \left( \frac{G M P^2}{4\pi^2} \right)^{1/3}, \]
  yielding the semi-major axis \( a \) as function of the period and total mass.
• Orbital Inclination (\( \iota \)): The angle between the orbital angular momentum vector and the line of sight to the observer. For \( \iota = 0 \), the binary is face-on, while for \( \iota = \pi/2 \), it is edge-on.

Step 2: Compute the Quadrupole Moment

The GW signal arises from the changing mass quadrupole moment. The orbit lies in a plane that can be tilted with respect to the observer's line of sight. For a general inclination, we first define the positions in the orbital plane and then transform to the observer's frame.

In the orbital plane (with center of mass at the origin), the positions are:

• WD 1 Position (\( \mathbf{r}_1 \)):
  \[ \mathbf{r}_1 = \left( \frac{M_2}{M} a \cos \omega t, \frac{M_2}{M} a \sin \omega t, 0 \right), \]
  where \( \frac{M_2}{M} a \) is the distance from the center of mass to WD 1.
• WD 2 Position (\( \mathbf{r}_2 \)):
  \[ \mathbf{r}_2 = \left( -\frac{M_1}{M} a \cos \omega t, -\frac{M_1}{M} a \sin \omega t, 0 \right), \]
  with \( \frac{M_1}{M} a \) as the distance to WD 2, and the negative sign ensuring the center of mass condition \( M_1 \mathbf{r}_1 + M_2 \mathbf{r}_2 = 0 \).

The mass quadrupole tensor is:

\[ I_{ij} = \sum_k m_k \left( r_k^i r_k^j - \frac{1}{3} \delta_{ij} r_k^2 \right), \]

where \( \delta_{ij} \) is the Kronecker delta, and \( r_k^2 = (r_k^x)^2 + (r_k^y)^2 + (r_k^z)^2 \). Compute key components:

• \( I_{xx} \):
  \[ I_{xx} = M_1 \left( \frac{M_2}{M} a \cos \omega t \right)^2 + M_2 \left( -\frac{M_1}{M} a \cos \omega t \right)^2, \]
  \[ = M_1 \frac{M_2^2 a^2 \cos^2 \omega t}{M^2} + M_2 \frac{M_1^2 a^2 \cos^2 \omega t}{M^2}, \]
  \[ = \frac{M_1 M_2^2 + M_2 M_1^2}{M^2} a^2 \cos^2 \omega t = \frac{M_1 M_2 (M_1 + M_2)}{M^2} a^2 \cos^2 \omega t, \]
  \[ = \mu a^2 \cos^2 \omega t. \]
  Adjust for the trace:
  \[ r_1^2 = \left( \frac{M_2}{M} a \right)^2 (\cos^2 \omega t + \sin^2 \omega t) = \left( \frac{M_2}{M} a \right)^2, \]
  \[ I_{xx} = \mu a^2 \cos^2 \omega t - \frac{1}{3} \mu a^2 \delta_{xx} = \mu a^2 \left( \cos^2 \omega t - \frac{1}{3} \right). \]
• \( I_{yy} \):
  \[ I_{yy} = \mu a^2 \sin^2 \omega t - \frac{1}{3} \mu a^2 = \mu a^2 \left( \sin^2 \omega t - \frac{1}{3} \right). \]
• \( I_{xy} = I_{yx} \):
  \[ I_{xy} = M_1 \left( \frac{M_2}{M} a \cos \omega t \right) \left( \frac{M_2}{M} a \sin \omega t \right) + M_2 \left( -\frac{M_1}{M} a \cos \omega t \right) \left( -\frac{M_1}{M} a \sin \omega t \right), \]
  \[ = \mu a^2 \cos \omega t \sin \omega t. \]

Step 3: Second Time Derivative of the Quadrupole Moment

GWs depend on the second time derivative \( \ddot{I}_{ij} \):

• \( \ddot{I}_{xx} \):
  \[ \dot{I}_{xx} = \mu a^2 \frac{d}{dt} (\cos^2 \omega t) = \mu a^2 \cdot 2 \cos \omega t (-\omega \sin \omega t) = -2 \mu a^2 \omega \cos \omega t \sin \omega t, \]
  \[ \ddot{I}_{xx} = \frac{d}{dt} (-2 \mu a^2 \omega \cos \omega t \sin \omega t), \]
  \[ = -2 \mu a^2 \omega \left[ (-\omega \sin \omega t) \sin \omega t + \cos \omega t (\omega \cos \omega t) \right], \]
  \[ = -2 \mu a^2 \omega^2 (-\sin^2 \omega t + \cos^2 \omega t) = -2 \mu a^2 \omega^2 \cos 2\omega t, \]
  using the identity \( \cos^2 \omega t - \sin^2 \omega t = \cos 2\omega t \).
• \( \ddot{I}_{yy} \):
  \[ \ddot{I}_{yy} = -\ddot{I}_{xx} = 2 \mu a^2 \omega^2 \cos 2\omega t, \]
• \( \ddot{I}_{xy} \):
  \[ \dot{I}_{xy} = \mu a^2 \frac{d}{dt} (\cos \omega t \sin \omega t) = \mu a^2 \left[ (-\omega \sin \omega t) \sin \omega t + \cos \omega t (\omega \cos \omega t) \right], \]
  \[ = \mu a^2 \omega (\cos^2 \omega t - \sin^2 \omega t) = \mu a^2 \omega \cos 2\omega t, \]
  \[ \ddot{I}_{xy} = \mu a^2 \omega \frac{d}{dt}(\cos 2\omega t) = \mu a^2 \omega (-2\omega \sin 2\omega t) = -2 \mu a^2 \omega^2 \sin 2\omega t. \]

Step 4: GW Strain Amplitude for Arbitrary Inclination

In the transverse-traceless (TT) gauge, the GW strain for an observer at inclination \( \iota \) is:

\[ h_{ij}^{\text{TT}} = \frac{2G}{c^4 D} \ddot{I}_{ij}^{\text{TT}}, \]

where \( c \) is the speed of light (\( 3 \times 10^8 \, \text{m/s} \)), and \( D \) is in meters.

When accounting for inclination \( \iota \), we need to project the quadrupole tensor onto the observer's reference frame. For an observer along a general direction, the two polarization components become:

\[ h_+ = \frac{G}{c^4 D} \mu a^2 \omega^2 (1 + \cos^2 \iota) \cos 2\omega t, \]

\[ h_{\times} = \frac{2G}{c^4 D} \mu a^2 \omega^2 \cos \iota \sin 2\omega t. \]

The overall GW strain amplitude scales as:

\[ h \sim \frac{G}{c^4 D} \mu a^2 \omega^2 \sqrt{(1 + \cos^2 \iota)^2 + 4\cos^2 \iota}. \]

Substitute \( a \) and \( \omega \):

\[ a^2 = \left( \frac{G M P^2}{4\pi^2} \right)^{2/3}, \]

\[ \omega^2 = \frac{4\pi^2}{P^2}, \]

\[ h \sim \frac{G}{c^4 D} \mu \left( \frac{G M P^2}{4\pi^2} \right)^{2/3} \frac{4\pi^2}{P^2} \sqrt{(1 + \cos^2 \iota)^2 + 4\cos^2 \iota}. \]

Simplify:

\[ h = \frac{G}{c^4 D} \mu (G M)^{2/3} \frac{4\pi^{2/3}}{P^{2/3}} \sqrt{(1 + \cos^2 \iota)^2 + 4\cos^2 \iota}. \]

Relate to GW frequency \( f = \frac{2}{P} \) (since GWs oscillate at twice the orbital frequency), so \( P = \frac{2}{f} \):

\[ P^{-2/3} = \left( \frac{2}{f} \right)^{-2/3} = \left( \frac{f}{2} \right)^{2/3}, \]

\[ h = \frac{G}{c^4 D} \mu (G M)^{2/3} 4\pi^{2/3} \left( \frac{f}{2} \right)^{2/3} \sqrt{(1 + \cos^2 \iota)^2 + 4\cos^2 \iota}. \]

Introducing the chirp mass:

\[ M_{\text{chirp}} = \frac{(M_1 M_2)^{3/5}}{(M_1 + M_2)^{1/5}} = \mu^{3/5} M^{1/5}, \]

the strain can be written in the standard form:

\[ h = \frac{4}{D} \left( \frac{G M_{\text{chirp}}}{c^3} \right)^{5/3} (\pi f)^{2/3} \mathcal{A}(\iota), \]

where \( \mathcal{A}(\iota) = \sqrt{(1 + \cos^2 \iota)^2 + 4\cos^2 \iota}/4 \) is the inclination-dependent amplitude factor.

Step 4b: Frequency Evolution and Chirp

While many WD binaries can be treated as monochromatic sources, some systems evolve measurably during observation. The orbital decay due to gravitational wave emission causes the frequency to increase over time, producing a "chirping" signal.

The energy loss due to gravitational wave emission is given by:

\[ \frac{dE}{dt} = -\frac{32}{5}\frac{G^4}{c^5}(M_1M_2)^2(M_1+M_2)\left(\frac{2\pi f_{\text{orb}}}{c}\right)^{10/3} \]

The orbital energy can be related to frequency:

\[ E = -\frac{G M_1 M_2}{2a} = -\frac{G M_1 M_2}{2}\left(\frac{G(M_1+M_2)}{4\pi^2}\right)^{1/3}(2\pi f_{\text{orb}})^{2/3} \]

Taking the time derivative and equating with the energy loss rate:

\[ \frac{dE}{dt} = -\frac{G M_1 M_2}{2}\left(\frac{G(M_1+M_2)}{4\pi^2}\right)^{1/3} \cdot \frac{2}{3} \cdot (2\pi)^{2/3} \cdot f_{\text{orb}}^{-1/3} \cdot \dot{f}_{\text{orb}} \]

Solving for \(\dot{f}_{\text{orb}}\):

\[ \dot{f}_{\text{orb}} = \frac{96}{5} \pi^{8/3} \left(\frac{G M_{\text{chirp}}}{c^3}\right)^{5/3} f_{\text{orb}}^{11/3} \]

For gravitational waves with \(f_{GW} = 2f_{orb}\):

\[ \dot{f}_{GW} = 2\dot{f}_{\text{orb}} = \frac{96\pi^{8/3}}{5 \cdot 2^{8/3}} \frac{G^{5/3}M_{\text{chirp}}^{5/3}}{c^5} f_{GW}^{11/3} \]

This frequency derivative is a strong function of both frequency and chirp mass, making it potentially detectable for higher frequency systems with larger masses.

Step 5: GW Polarizations with Inclination

The time-dependent GW polarizations for a binary with inclination \( \iota \) are:

\[ h_+ = h_0 \frac{1 + \cos^2 \iota}{2} \cos(2\pi f t + \pi\dot{f}t^2 + \phi_0), \]

\[ h_{\times} = h_0 \cos \iota \sin(2\pi f t + \pi\dot{f}t^2 + \phi_0), \]

where \( h_0 \) is the overall amplitude and \( \phi_0 \) is an initial phase. Note that for chirping sources, we've included the $\pi\dot{f}t^2$ phase term.

For different inclinations:

• Face-on (\( \iota = 0 \)):
  \[ h_+ = h_0 \cos(2\pi f t + \pi\dot{f}t^2 + \phi_0), \quad h_{\times} = h_0 \sin(2\pi f t + \pi\dot{f}t^2 + \phi_0) \]
  The GW has equal plus and cross polarizations, 90° out of phase, creating circular polarization.
• Edge-on (\( \iota = \pi/2 \)):
  \[ h_+ = \frac{h_0}{2} \cos(2\pi f t + \pi\dot{f}t^2 + \phi_0), \quad h_{\times} = 0 \]
  Only the plus polarization remains, creating linear polarization with reduced amplitude.

2. Extracting Distance and Position with LISA

LISA, with its \( a \approx 2.5 \times 10^9 \, \text{m} \) baseline, uses the GW signal to infer \( D \), sky position \( (\alpha, \delta) \), and inclination \( \iota \).

Distance (\( D \)) and Inclination (\( \iota \))

From:

\[ h = \frac{4}{D} \left( \frac{G M_{\text{chirp}}}{c^3} \right)^{5/3} (\pi f)^{2/3} \mathcal{A}(\iota), \]

LISA measures \( h_+ \) and \( h_{\times} \) separately, allowing determination of both \( D \) and \( \iota \) through:

\[ \frac{h_{\times}}{h_+} = \frac{2\cos \iota}{1 + \cos^2 \iota}, \]

which gives \( \iota \), and then:

\[ D = \frac{4 \mathcal{A}(\iota)}{h} \left( \frac{G M_{\text{chirp}}}{c^3} \right)^{5/3} (\pi f)^{2/3}. \]

Note that for purely monochromatic sources, $M_{\text{chirp}}$ remains degenerate with distance, and may require electromagnetic counterparts or statistical priors to determine independently.

Chirp Measurement and Distance Precision

For binaries where LISA can measure \(\dot{f}_{GW}\), the chirp mass can be determined independently:

\[ M_{\text{chirp}} = \left(\frac{5c^5}{96\pi^{8/3}} \cdot \frac{\dot{f}_{GW}}{f_{GW}^{11/3}} \cdot \frac{2^{8/3}}{G^{5/3}}\right)^{3/5} \]

This breaks the degeneracy between chirp mass and distance, allowing for direct distance determination:

\[ D = \frac{4 \mathcal{A}(\iota)}{h} \left( \frac{G M_{\text{chirp}}}{c^3} \right)^{5/3} (\pi f)^{2/3} \]

LISA can typically detect frequency evolution when:

• The frequency shift over the observation period is larger than the Fourier bin width: $\dot{f}_{GW} \cdot T_{obs}^2 > 1$
• The signal-to-noise ratio is sufficient (typically SNR $\gtrsim$ 20)
• The binary has higher frequency ($f_{GW} \gtrsim 3$ mHz) and/or larger chirp mass

The precision in distance determination improves dramatically when $\dot{f}_{GW}$ is measurable:

\[ \frac{\sigma_D}{D} = \sqrt{\left(\frac{\sigma_h}{h}\right)^2 + \left(\frac{5}{3}\frac{\sigma_{M_{\text{chirp}}}}{M_{\text{chirp}}}\right)^2} \]

For typical WD binaries at mHz frequencies with 4-year observation times, distance precision can improve from factors of many tens of percent to approximately 10-30% when $\dot{f}_{GW}$ is detectable.

Sky Position (\( (\alpha, \delta) \))

LISA leverages several effects for sky localization:

• Doppler Modulation:
  \[ f_{\text{obs}} = f \left(1 + \frac{\mathbf{v} \cdot \mathbf{n}}{c} \right), \]
  where \( \mathbf{v} \) is LISA's orbital velocity (~30 km/s around the Sun), and \( \mathbf{n} \) is the unit vector to the source, modulating \( f \) over its 1-year orbit.
• Amplitude Modulation:
  \[ h(t) = F_+ h_+ + F_{\times} h_{\times}, \]
  where \( F_+, F_{\times} \) are antenna pattern functions depending on \( (\alpha, \delta) \) and LISA's orientation.
• Sky Localization Area: For short observations, the resolution is limited by the detector arm length \( a \):
  \[ \Delta \Omega_{\text{short}} \sim \frac{1}{\text{SNR}^2} \left( \frac{\lambda}{a} \right)^2, \quad \lambda = \frac{c}{f}, \]
  But for long-term observations (≈1 year), LISA's orbital motion provides an effective baseline of \( 2 R_{\text{orbit}} \) (≈ 2 AU):
  \[ \Delta \Omega_{\text{long}} \sim \frac{1}{\text{SNR}^2} \left( \frac{\lambda}{2 R_{\text{orbit}}} \right)^2 \]
  where SNR is the signal-to-noise ratio, and \( \lambda \) is the GW wavelength.

Example Calculation

For \( f = 1 \, \text{mHz} \) and short-term observations with LISA's arm length \( a \approx 2.5 \times 10^9 \, \text{m} \):

\[ \lambda = \frac{3

Possible Masters Projects

Project 1: 

The Dynamical Structure and Population of the Extremely Metal-Rich "Knot" at the center of the Milky Way 

Background

The Milky Way's formation history is encoded in the distribution of stellar orbits -- ages -- and chemical abundances. They are the key to: how many stars formed when from what material? Gaia and spectroscopic surveys such as SDSS/APOGEE make it now possible to draw up such map for the full galaxy. 

Given that the element abundances are permanent 'birth tags' it makes sense to ask what the spatial (or orbit) distribution of 'mono-abundance' populations is. In recent work, we have found/discovered that the extremely metal rich stars in our Galaxy mostly form an extremely metal-rich (EMR) knot at the center of the Milky Way.

All-sky maps of the stellar density for very metal-rich stars in the inner Galaxy (from Rix+2024). Note that the extremely metal-rich stars (EMR; bottom panel) are largely confined to a central "knot".

In light of this finding, some questions are:

• did the stars form there?
• on what orbits are they? radial, rotating, etc..
• how old are they? (did they form in several episodes)

We have initial kinematics, that point to radial, centrally confined orbits.

The current analyses are limited by a) dust (when considering radial velocities from Gaia), and b) by modest sample size, when considering SDSS IV/APOGEE spectra.

Goal

In the context of SDSS-V we are getting (and have gotten) many more spectra towards the central 1.5 kpc. The central goal of the masters project is to take these, potentially do some post-processing on them, and build a kinematic/dynamical model for the extremely metal-rich central knot.

(possible) steps

• collect all data (velocities, metallicities) of existing and new SDSS/APOGEE spectra in the inner 1.5 kpc of the Milky Way
• find the very metal rich ones
• get the best possible distances of these stars (Gaia and spectroscopic information)
• combine SDSS/APOGEE information with Gaia to determine orbits
• determine orbit distribution, mostly the distribution in binding energy (or apocenter) and eccentricity.
• build a simple dynamical model.
• determine the spatial and orbit distribution, and (optional) compare it to TNG50 Milky Way formation simulations.

Tools

• working with the sloan data base
• working with python dynamics packages such as galpy
• writing a set of jupyter notebooks (or other forms of python code) to do further analysis and make plots.

Hoped-For Outcome

Leading a refereed population on this analysis

Project 2: 

Mapping the Metallicity of Young Stars across the Milky Way Disk

or: how homogeneous is the birth material of stars at a given time and radius?

Background

We have reason to believe that the interstellar medium -- from which stars form -- is nearly homogeneous in azimuth, at a given radius and time in the life of a galaxy: at any given epoch, a star's chemical abundances only depend on the radius at which it was born. It would be important to test this hypothesis, as it is a starting point for understanding many evolutionary mechanisms in disk galaxies (e.g. radial migration). The way one could do this is to find young stars (say, less than an orbital period, or 250Mio yrs) luminous to be seen across the disk) and measure their abundances, to see whether this important assumption about "chemical homogeneity" is true.

What to take for young luminous stars: the easiest would be to take hot young stars (OB stars); but they have few metal lines, so it is hard to measure [Fe/H]. But all stars (>Mio years) have a red giant phase, where they are cool enough to yield metallicities. 

Goal

The goal is to find (among the 10 Mio) the red giants with [M/H] from Gaia the ones that are <200Mio old, and map their metallicities: are there azimuthal variations?

How: the two plots below show that the temperatures and luminosities of giants depend on age, and metallicity. If one know the metallicity, one gets the age:

CMD positions of red giants with solar metallicity, but different ages

CMD positions of stars of 10^9 years age, but of different
metallicities. Age and metallicity are covariant.

We have developed a piece of code (for application in the LMC) that takes the distances, magnitudes, metallicities and temperatures of giants and determines their ages.How: the two plots below show that the temperatures and luminosities of giants depend on age, and metallicity. If one know the metallicity, one gets the ages.

Goal (possible) steps

• take intellectual ownership of the age fitting code (with some possible tweaks/checks)
• collect the data (from Gaia; catalogs exist) of the stellar parameters for all "Gaia giants with spectroscopy". find the subset with good distances, and apply age-fitting code.
• find the young giants
• make metallicity maps
• take it from there..

Tools

• working with Gaia and zenodo data base
• learn and adopt a piece of existing code
• writing a set of jupyter notebooks (or other forms of python code) to do further analysis and make plots.

Hoped-For Outcome

Leading a refereed population on this analysis

Thoughts on Wide-Field Slitless Spectroscopy from Space

 Slit-less Survey Spectroscopy from Space

This reflects some rambling thoughts that HWR has harboured over the last years on the question of what's the ultimate all-sky spectroscopic survey. Given that there is much (MEGAMAPPER, MSE, ..) pondering about the ground-based options, this is about space (inspired by the Gaia, JWST and Euclid slitless data).

To cut long story short. One dream-option could be:

• let's presume a 6.5m (warm?) telescope could be designed [credit to Roger Angel here] with a near diffraction limited  0.25 (or 1) sqdeg FOV in a TESS-like or L2 orbit ; 
• and if one could then implement slitless spectroscopy with a resolution R (say R=1000, or 2000?), and a bandpass filter that picks out NR (say NR=1000, or 2000?) resolution elements
• the actual wavelength requires a great deal of thought, but let's take here 0.8mum-1.6mum
• Notes:
• a 1sqdeg FOV would require about 20 Gpixels (same as imaging at the same resolution and FOV); so, thinking about undersampling, or 0.25sqdeg may make this idea less pie-in-the-sky
• note that the number of pixels needed is the same as for direct imaging; it's just imaging with every source being a short streak 
• How long is the slitless spectral streak in the focal plane?  for NR resolution elements, the streak is NR * FWHM(PSF)  = 47" at NR=1000; lambda=1.5mum, D=6.5m
• then obvious science include (see section below the S/N estimates for more/growing detail). Brief quip:  that MSE, SpecTel, Roman, etc.. just much better.
• stellar physics
• Galactic history, structure and dynamics
• redshift surveys
• AGN finding
• good angular resolution
• spectral "follow-up" on LISA GW sources
• to cover a good portion of the sky "in a reasonable period" (few years?), exposure times per pointing 1000s-ish?

Why would that be a dream? 

The S/N estimates written out below illustrate the power that arise from combining:

• slitless (you get everything)
• observations from space (low background)
• a large and diffraction limited telescope
• compact sources (the last two boost the source/background contrast)

• 

Survey speed (to a given depth) for faint, compact sources scales with telescope size as D^4.

[This can do (more) in one year than Roman (slitless) in 50 years]

In addition, the probability of source confusion (at given R, and NR) goes down as D^-2.

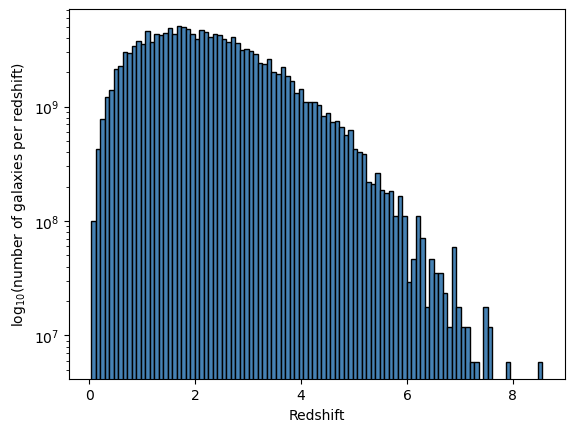
Here are some plots that show an initial S/N estimate exercise. Given that the background tends to kill you in slitless spectroscopy, compact sources (PSF) are great.

Anyone who wants to play with S/N matters, go to the collab notebook here

This shows at R=1000, 1.5mum the continuum S/N (per resolution element) in a 1000 second exposure for sources of different spatial extent, as a function of their size (source diameter)

This shows the S/N (per resolution element) for a continuum point source, as a function of telescope diameter. For reference, Euclid~1m, Roman~2.4m

This is an analogous plot, but for a (spectrally) unresolved emission line on top of negligible source continuum. The envisioned line-flux sensitivity for ground-based "stage 5" redshift experiments (0.5e-16) is indicated (see https://arxiv.org/pdf/2209.03585.pdf )

This is a first attempt at mapping the S/N to some physical input, such as a star-forming region/galaxy as a function of of their size and SFR. Yes, spatial extendedness is a killer.

=======

Reminder 1: what is the physical resolution as a function of redshift

=======

Just as background, here's the sky values from Rigby+2023

Science Cases with such a Survey:

This deserves simulations and asking what range of lambda,R,NR, etc.. is optimal, and which acceptable

Spectra of Stars:

• 2-5 abundances of cool stars
• are there any zero-metallicity stars in the Milky Way?
• chemical identification of streams (as small-scale DM probes)
• find the fastest stars (in the bulge): BH dynamics
• spectra of every O stars within 5 Mpc
• free-floating (semi-young) planets and stuff

Spectra of AGNs:

• AGN as LSS probes to z=7(?)
• earliest AGN (z~12) ==> BH growth; seed BHs

Spectra of Galaxies 

What can we expect for emission line spectroscopy of galaxies?

Let's take the Yung, Somerville+2022 SC-SAM simulations, and the Kennicutt

conversion of SFR --> Halpha; and request a 7 sigma Halpha detection, given line flux and disk-size of the galaxy. Consider a total area of 10.000 sqdeg on the sky. Quite staggering galaxy numbers ....

• ?? <what are the most interesting things>
• host galaxy diagnostics of BH GW events with LISA

Cosmology:

• probes of inflationary signatures (by stage 5+ spectroscopy)

• kinematic lensing on steroids
• 
  

(inadvertent) Spectra of Transients

• way too many gravitational lenses with spectra
• serendipidous (single epoch) SN spectra to faint levels
• GRB hosts
• tidal disruption events in AGN
• <you name it>

Low-mass objects

• there are ATMO2020 models from Phillips+2020 and newer (JWST-oriented) models Legget&Tremblin 2024
  
  
  

from Theissen, Burgasser et al 2023.  LTY dwarf spectral library

How many more stars (for stellar streams) does one get going below the MS turn-off
(from Bellazini+ https://arxiv.org/abs/1203.3024) 

going from absmag 2 (in I) to 3 is 20x more stars

Notes on crowding:

I downloaded Gaia data in Baade's window, and did number counts, which resulted in an estimate of how many stars there are per spectral streak area (code at getBaadesWindow.ipynb) in 

/Users/rix/Science/Projects/SlitlessSpectroscopySpace/SpectraSims

The plots looks like this, and implies that the crowding is unproblematic to 21st magnitude

Next steps would be to 

a) get deeper data

b) calculate the Poisson probability of being uncontaminated and add it to that plot.

More science application ideas

The universe through a looking-glass

Strong (>30) lensing magnification (size and flux) happens, by is rare. When it happens, it opens up a new regime of spatial resolution.

Takahashi et al 2011 have calculated statistics. The plot below shows magnification averaged over 3kpc

For compact sources there should be much more magnification.

Extreme magnification probabilities have been discussed in Diego (2019)

So, there is a 1 in a million chance to get magnification of more than a 1000. A linear magnification of 20 leads to a physical resolution (6.5m at 0.75mum) of 9 pc at z=5.

Possible next steps in XP spectra & the Milky Way

 These are literally only notes-to-self by HW

The Rich Heart of the Milky Way

[see also the Jupyter notebook: Metal Rich Stars from Andrae+2023]

I just made the plot using the Andrae+2023 giant table

We can then identify the most metal-rich stars in it [M/H]>0.47.

Their CMD's look "normal"; but iffy [M/H]-estimates and imprecise parallaxes

prevent clear age-dating.

We then look at the all-sky distribution, in different metallicity slices, which looks remarkable

 To do's:

• plot [M/H]_XP vs DR17 APOGEE - get new metallicities from Andy Casey (?)
• check whether there are any RV's (few?)
• get good distances (a la Hogg...) or from Xiangyu
• with good/assumed distances, say something about the ages
• build a model to constrain the level of rotation using only proper motions (that needs good distances). -- get proper motions!! (the notebook is set up for that)
• all this requires a clean-up/augmentation of the Jupyter notebook.

Giant Ages within 3 kpc

For giants with XP metallicities and very good parallaxes (5%?) we can get ages, as in the LMC, using HWR's sped-up code.   We should do that..  perhaps suggest to to Josh?

Calibration of the stellar mass scale on the lower MS

I have taken the Hwang et al 2023 code that calculates (and dynamically calibrates) M_*(absG,B-R) from the wide-binary dynamics and applied it to M-dwarfs. Compared to the what the Carmenes DR1 folks use, there is a serious offset.